Metadata
aliases: []
shorthands: {}
created: 2021-10-31 15:38:01
modified: 2022-01-10 04:13:03
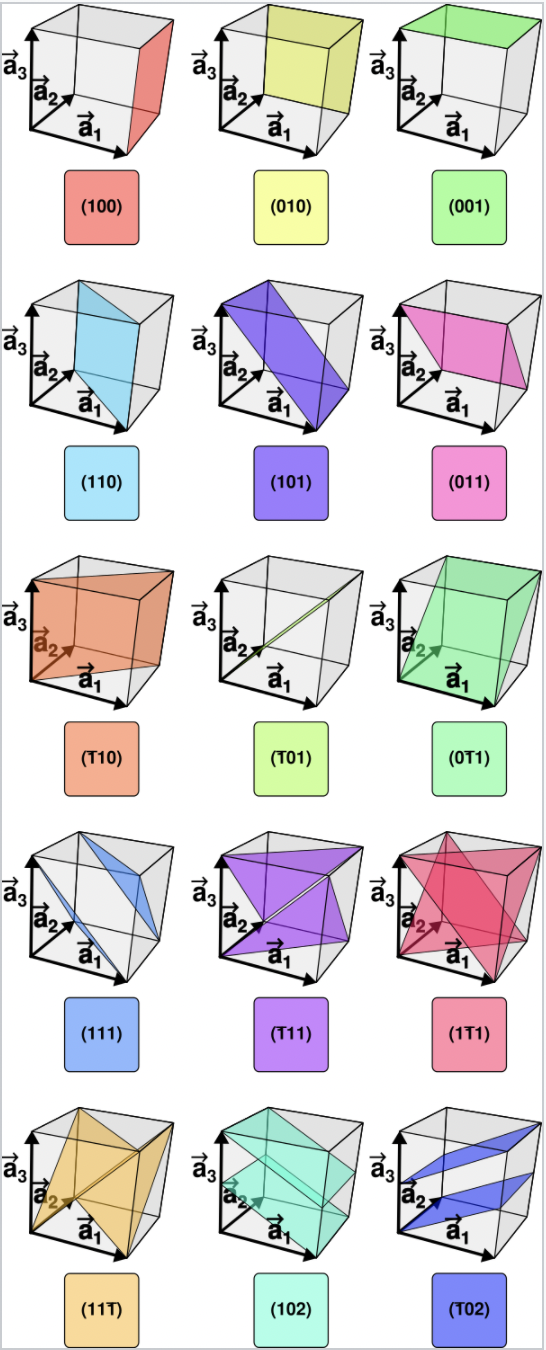
A lattice place of a given Bravais lattice is a plane containing at least three noncolinear Bravais lattice points. A lattice plane's intersection with the lattice is always periodic (described by a 2D Bravais lattice).
All lattice planes can be described by a set of integer Miller indices and vice versa.
Conversely, planes that are not lattice planes have aperiodic intersections with the lattice, called quasicrystals.
Lattice planes with different Miller indices in cubic crystals:
